Pyzo

Cette page présente le calcul numérique de la dérivée d'une fonction :\(y_i\) dont on connaît les valeurs pour des abscisses\(x_i\) .

Une approximation numérique de la dérivée est obtenue en calculant la pente entre deux points de coordonnées\((x_i , y_i)\) et\((x_{i+1} , y_{i+1})\)

La pente correspond au coefficient directeur de la droite qui passe par ces deux points.

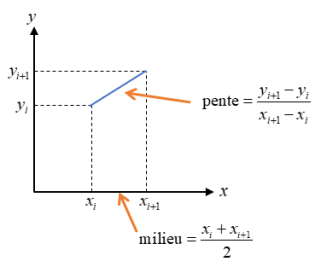
Comme la pente est calculée entre deux abscisses\(x_i\) et\(x_{i+1}\) , on associera cette dérivée à l'abscisse située au milieu.

On stocke les valeurs des nouvelles abscisses dans un tableau\(xnew\) avec\(xnew_i= \frac{x_i+x_{i+1}}{2} \).

Il est important de noter qu'il y aura seulement\(len(x)-1\) valeurs pour\(xnew\).

On utilise une boucle pour calculer les valeurs de la dérivée qui seront stockées dans un tableau\(dy\) (d pour la dérivée) avec\(dy_i= \frac{y_{i+1}-y_i}{x_{i+1}-x_i}\)

## Définition de la fonction dérivation

def derivation(x,y):

# x et y des listes ou des tableaux de valeurs, de même dimension

# xnew et dy les tableaux de valeurs de la nouvelle abscisse et de la dérivée

xnew=np.zeros(len(x)-1)

dy=np.zeros(len(x)-1) # tableau de zéros pour la dérivée dy

for i in range(len(x)-1):

xnew[i] = (x[i] + x[i+1]) / 2

dy[i] = (y[i+1] - y[i]) / (x[i+1] - x[i])

return (xnew,dy)

Exemple d'utilisation de cette fonction :

# t, x sont les tableaux des valeurs brutes de même dimension

# v est le tableau des valeurs dérivées

(tnew,v)=derivation(t,x)

## Définition de la fonction dérivation

def derivation(x,y):

# x et y des listes ou des tableaux de valeurs, de même dimension

# dy le tableau de valeurs de la dérivée

n=len(x)

dy=np.zeros(n) # tableau de n zéros pour la dérivée dy

# premier point : dérivée à droite -> : f'(xi)=(f(xi+h)-f(xi))/h)

dy[0]=(y[1]-y[0])/(x[1]-x[0])

# dérivée centrée pour les autres points -> : f'(xi)=(f(xi+h)-f(xi-h))/(2*h)

for i in range(1,n-1):

dy[i]=(y[i+1]-y[i-1])/(x[i+1]-x[i-1])

#dernier point : dérivée à gauche -> : f'(xi)=(f(xi)-f(xi-h))/h

dy[n-1]=(y[n-1]-y[n-2])/(x[n-1]-x[n-2])

return dy

Exemple d'utilisation de cette fonction :

# t, x sont les tableaux des valeurs brutes de même dimension

# v est le tableau des valeurs dérivées

v=derivation(t,x)